Environment
Your task is to develop a controller for a physiologically plausible 3D human model to move (walk or run) following velocity commands with minimum effort.
Formally, you build a policy \(\pi:V \times S \rightarrow A\) from the body state \(S\) and target velocity map \(V\) to action \(A\).
The performance of your policy will be evaluated by the cumulative reward \(J(\pi)\) it receives from simulation.
The evaluation environment for Round 1 is set as model='3D', difficulty=2, project=True, and obs_as_dict=True.
Human Model
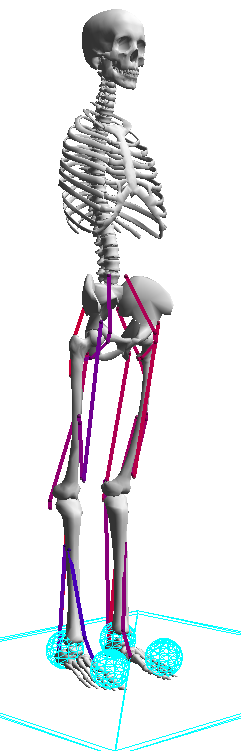
- \(3D\) musculoskeletal model of healthy adult
- \(8\) internal degrees of freedom (4 per leg)
- hip_abd (+: hip abduction)
- hip (+: extension)
- knee (+: extension)
- ankle (+: plantar flexion)
- \(22\) muscles (11 per leg)
- HAB: hip abductor
- HAD: hip adductor
- HFL: hip flexor
- GLU: glutei (hip extensor)
- HAM: hamstrings (biarticular hip extensor and knee flexor)
- RF: rectus femoris (biarticular hip flexor and knee extensor)
- VAS: vastii (knee extensor)
- BFSH: biceps femoris, short head (knee flexor)
- GAS: gastrocnemius (biarticular knee flexor and ankle extensor)
- SOL: soleus (ankle extensor)
- TA: tibialis anterior (ankle flexor)
Evaluation
- Round 1 will be evaluated with model=3D and difficulty=2, where difficulty sets the level of the target velocity map.
- Evaluation of Round 2 will be determined based on the leading teams performance in Round 1.
Reward
Round 1
A simulation runs until either the pelvis of the human model falls below \(0.6\) meters or when it reaches \(10\) seconds (\(i=1000\)). During the simulation, you receive a survival reward every timestep \(i\) and a footstep reward whenever the human model makes a new footstep \(step_i\). The reward is designed so that the total reward \(J(\pi)\) is high when the human model locomotes at desired velocities with minimum effort.
The footstep reward \(R_{step}\) is designed to evaluate step behaviors rather than instantaneous behaviors, for example, to allow the human model’s walking speed to vary within a footstep as real humans do. Specifically, the rewards and costs are defined as
\(\Delta t_{i}=0.01\) sec is the simulation timestep, \(v_{pel}\) is the velocity of the pelvis, \(v_{tgt}\) is the target velocity, \(A_{m}\)s are the muscle activations, and \(w_{step}\), \(w_{vel}\) and \(w_{eff}\) are the weights for the stepping reward and velocity and effort costs.
Round 2
There are some changes for Round 2:
- Task bonus, \(R_{target}\)
- You will get this large bonus if the human model stays near the target for enough time (2~4 sec)
- You can get this bonus 2 times in one trial: If you obtain the first one, a new target will be generated (i.e. target velocity map will change).
- Maximum simulation time is \(25\) seconds (\(i=2500\))
- The time is enough that a successful solution will be one that reaches and stays at the second target. This will avoid the issue of the successful solution terminating at an arbitrary gait phase, which results in a small but arbitrary difference in the reward.
Observation (input to your controller)
The observation or the input to your controller consists of a local target velociy map \(V\) and the body state \(S\).
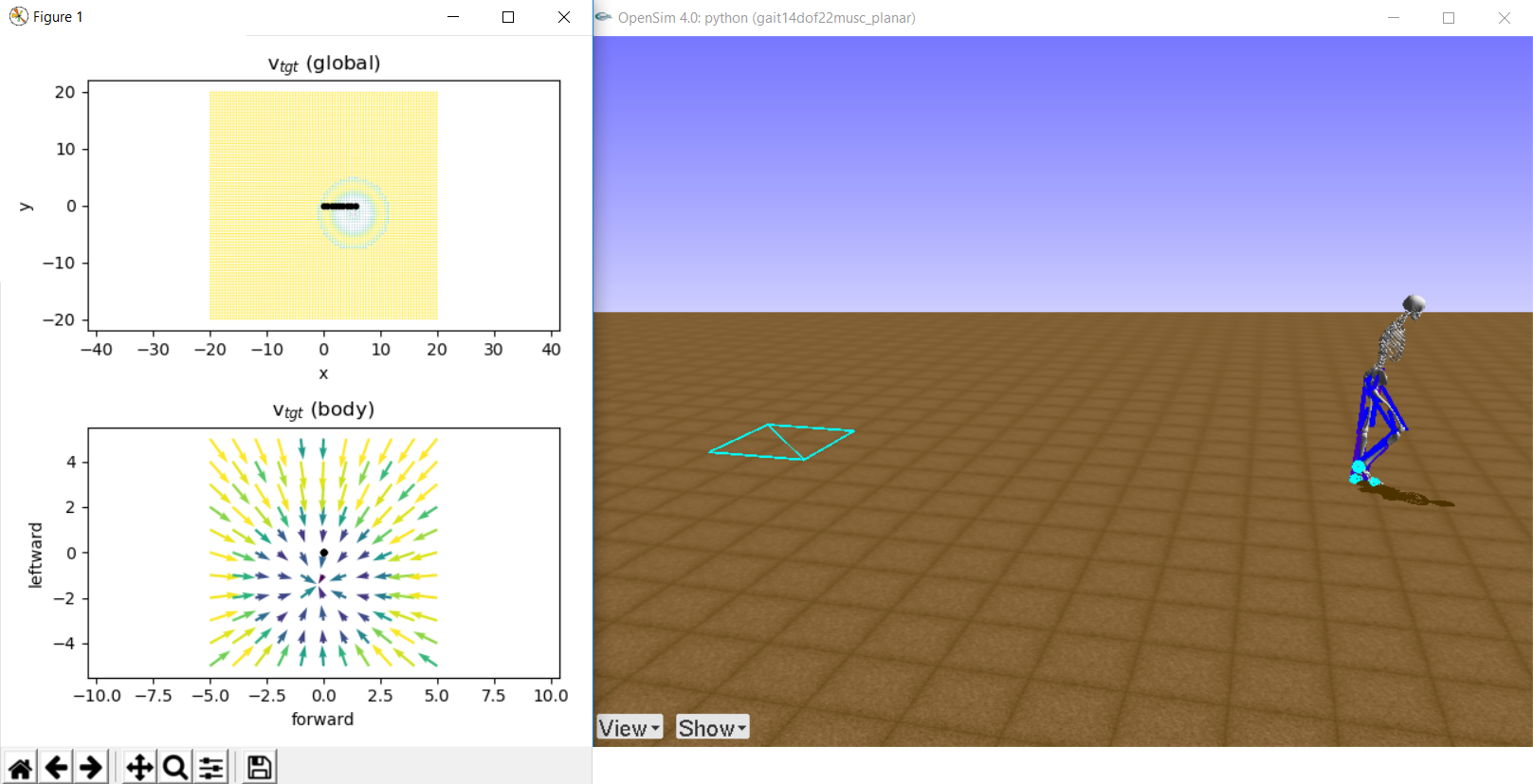
\(V\) is a \( 2 \times 11 \times 11 \) matrix, representing a \(2D\) vector field on an \(11 \times 11 \) grid. The \(2D\) vectors are target velocities, and the \(11 \times 11 \) grid is for every \(0.5 \) meter within \(\pm 5\) meters back-to-front and left-to-side. For example, in the figure below, the global target velocity map (top-left) shows that the velocity field converges to \((5.4, -1.4)\) and the human model is at \((5.4, 0.0)\) (end of the black line). Thus, the local target velocity map (bottom-left) shows that the human model should locomote to the right as the target velocity vector at \((0.0, 0.0)\) points towards the right (i.e. close to \([0, -1]\)).
Target positions (the velocity sinks) in Round 1 are generated at the right side of the human model ( \(x_{tgt} > (x_{pel}\) ), while they generated in any directions in Round 2. Test the target velocity map:
python -m envs.target.test_v_tgt
 |
\(S\) is a \(97D\) vector representing the body state. It consists of pelvis state, ground reaction forces joint angles and rates and muscle states. The keys of the observation dictionary should be self evident what the values represent.
Action (output of your controller)
The action space \([0,1]^{22}\) represents muscle activations of the \(22\) muscles, 11 per leg.
Submission
There are two ways to submit your solutions:
- Option 1: submit solution in docker container
- Option 2: run controller on server environment